Multi-Class Confusion Matrices
This pages describes confusion matrices for multi-class / select tasks. While this description is for multi-select classification, it is relevant for multi-class segmentation and range selection as well.
Overview of True / False Positive and True / False Negative
Multi-select classification can be viewed as a series of binary decisions. For example, in a task where people classify images of animals with possible labels (Dog, Cat, Bird), they are effectively responding to three binary questions: (1) “Is the animal a dog?”, (2) “Is the animal a cat?”, and (3) “Is the animal a bird?”. Whichever class is included in the majority labels is the Positive class and the remaining classes not included in the majority label are the Negative classes. The table below illustrates this for a case where the majority label is Dog.
| Label | Is the label included in the majority label? | Positive or Negative |
|---|---|---|
| Dog | Yes | Positive |
| Cat | No | Negative |
| Bird | No | Negative |
- If the positive class is also included in the correct label, this response is categorized as a True Positive.
- If the positive class is not included in the correct label, this response is categorized as a False Positive.
- If the negative class is also not included in the correct label, this response is categorized as a True Negative.
- If the negative class is included in the correct label, this response is categorized as a False Negative.
The table below illustrates the response categories for a case where the majority label is Dog and the correct label is Dog:
| Label | Is the label included in the majority label? | Is the label included in the correct label? | Does the majority label match the correct label? | Response Category |
|---|---|---|---|---|
| Dog | Yes (positive) | Yes | True | True positive |
| Cat | No (negative) | No | True | True negative |
| Bird | No (negative) | No | True | True negative |
Similarly, the table below illustrates the response categories for a case where the majority label is Dog and the correct label is Cat:
| Label | Is the label included in the majority label? | Is the label included in the correct label? | Does the majority label match the correct label? | Response Category |
|---|---|---|---|---|
| Dog | Yes (positive) | No | False | False positive |
| Cat | No (negative) | Yes | False | False negative |
| Bird | No (negative) | No | True | True negative |
The two tables illustrate the different patterns of response categories that arise from correct and incorrect responses in multi-label classification tasks. With a correct answer, one label is categorized as a True Positive and the remaining labels are categorized as True Negatives. With an incorrect answer, one label is categorized as a False Positive, one label is categorized as a False Negative, and the remaining labels are categorized as True Negatives.
Confusion Matrix Overview
A confusion matrix is designed to illustrate the patterns of true positives, false positives, and false negatives because the matrix contains one element for each possible combination of (correct label, majority label). Diagonal elements of the matrix denote correct responses (true positives), where the correct label is equal to the majority label, and off-diagonal elements denote incorrect responses, where the correct label is not equal to the majority label. In the latter case, the correct label is a false negative and the majority label is a false positive. Therefore, each off-diagonal element simultaneously encodes both a false negative and a false positive.
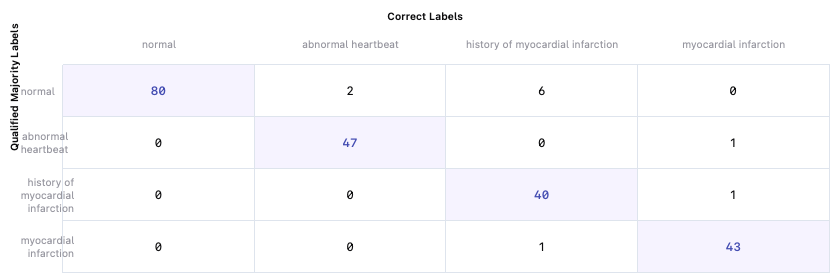
Multi-select / Multi-class Confusion Matrices
For multi-select classification tasks, we use two confusion matrices to illustrate patterns of true positives, false positives, and false negatives.
Why the need for two matrices?
As stated previously, the off-diagonal elements of the traditional confusion matrix simultaneously encode a false negative and a false positive. Therefore, the traditional single-matrix representation is only appropriate when there is a false negative if and only if there’s a false positive. In multi-select classification tasks, false negatives can arise without false positives and vice-versa. The illustration below provides examples of how this could occur in a task where people classify images of animals with possible labels (Mammal, Dog, Spotted).

Possible labels: Mammal, Dog, Spotted
Example 1: If the majority label is (Mammal) and the correct label is (Mammal, Dog), then Dog is a false negative and there is no false positive.
Example 2: If the majority label is (Mammal, Dog, Spotted) and the correct label is (Mammal, Dog), then there is no false negative and Spotted is a false positive.
While there has been some research devoted to using a single-matrix representation to illustrate confusion matrix information for multi-select classification tasks (Hedaryian et al., 2022; Kristinic et al. 2020; Kristinic et al., 2023), Kristinic et al. (2024) instead propose to decompose the confusion matrix into two matrices, one which encodes false positive information (the precision matrix) and one which encodes false negative information (the recall matrix). We take a similar approach to Kristinic et al. (2024) when displaying confusion matrix information for multi-select classification tasks in our portal.
Below is how the precision and recall matrices would depict Example 1 where the majority label is (Mammal) and the correct label is (Mammal, Dog)
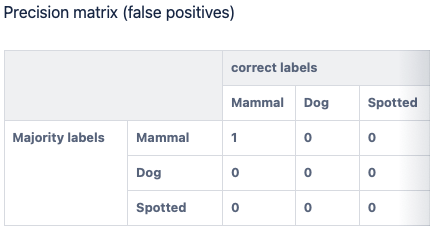
Because there is no false positive, the precision matrix has 0 for all off-diagonal elements.

But, because there is a false negative, the recall matrix has a 1 in one of the off-diagonal elements (correct label = Dog, majority label = Mammal). For this instance, the non-zero off-diagonal element in the recall matrix signifies that when Dog was incorrectly omitted from the majority label (a false negative), Mammal was included in the majority label.
In both matrices, there is a 1 at (correct label = Mammal, majority label = Mammal) because Mammal was included in both the correct label and the majority label.
Below is how the precision and recall matrices would depict Example 2 where the majority label is (Mammal, Dog, Spotted) and the correct label is (Mammal, Dog)
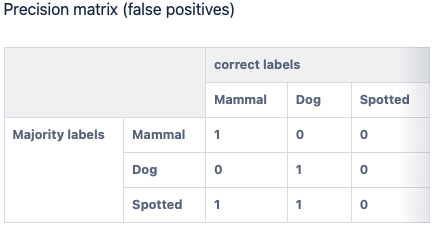
Because there is a false positive, the precision matrix has a 1 at (correct label = Mammal, majority label = Spotted) and at (correct label = Dog, majority label = Spotted). For this instance, the non-zero off-diagonal elements in the precision matrix indicate that when Spotted was incorrectly included in the majority label (a false positive), both Dog and Mammal were included in the correct label.
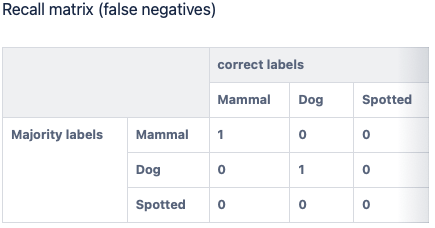
Because there is no false negative, the recall matrix has 0 for all off-diagonal elements.
In both matrices, there is a 1 at (correct label = Mammal, majority label = Mammal) and (correct label = Dog, majority label = Dog) because both Mammal and Dog were included in both the correct label and the majority label.
How would these matrices be interpreted at the group level?
Below is an example of what the total precision and recall matrices could look like at the group level with their interpretations.
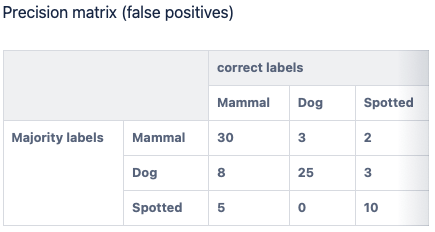
Using the (correct label = Mammal, majority label = Spotted) element, the precision matrix tells us that there are 5 instances where the majority label incorrectly included Spotted (a false positive) and the correct label included Mammal. Note, this does not necessarily mean that Mammal was a false negative, as the correct label could have also included Mammal. The purpose of the precision matrix is to illustrate which classes were included in the correct label when a false positive occurred.

Using the (correct label = Mammal, majority label = Spotted) element again, the recall matrix tells us that there are 7 instances where the majority label incorrectly omitted Mammal (a false negative) and the majority label included Spotted. Note, this does not necessarily mean that Spotted was a false positive, as the majority label could’ve also included Spotted. The purpose of the recall matrix is to illustrate which classes were included in the majority label when a false negative occurred.
Tips to Read Matrices at a Glance:For the precision matrix, focus on the majority label row for each off-diagonal element to determine which classes were incorrectly included in the majority label as false positives.
For the recall matrix, focus on the correct label column for each off-diagonal element to determine which classes were incorrectly omitted from the majority labels as false negatives.
Range and Segmentation:
The two matrices are also used for range and segmentation tasks. If the majority range/segmentation annotation includes at least one finding for a given label class, then that class is included in the majority label. If not, then that class is not included in the majority label. The correct label is generated in the same manner. Using these correct and majority labels, the confusion matrix is computed in the same manner as in a multi-select classification task.
Updated 5 months ago
